The assignment of PHY2709 Quantitative Biology. It is a brief paper reading report of Ozbudak EM, Thattai M, Lim HN, Shraiman BI, Van Oudenaarden A. Multistability in the lactose utilization network of Escherichia coli. Nature. 2004 Feb 19;427(6976):737-40. doi: 10.1038/nature02298. PMID: 14973486.
Model (Conceptual)
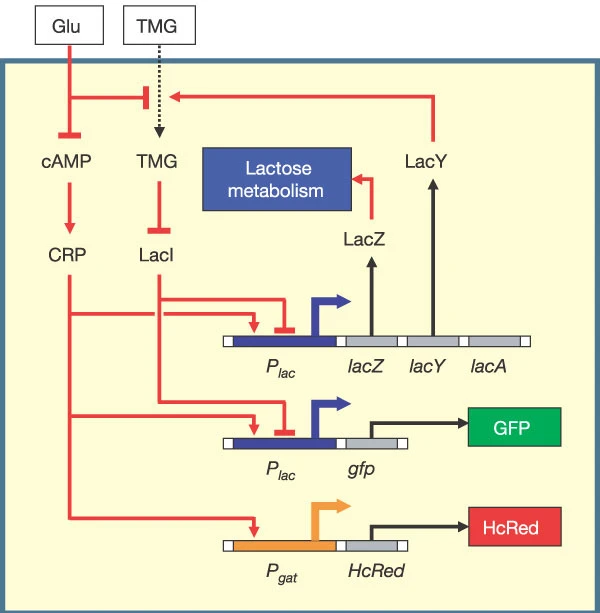
E. coli uses multiple carbon sources, i.e. glucose, lactose, etc. This is the lactose utilization network. The lac operator regulates the production of the substances related to lactose metabolism. LacY, TMG and LacI form a positive feedback loop in the network, which is essential for multistability behavior. In the experiment, researchers used two fluorescent to decouple the effects from cAMP-CRP and TMG-LacI. The two input parameters of the network are the external concentration of glucose and TMG (intuitively, it represents the constitution of the carbon sources).
Saddle-node bifurcation and bistability
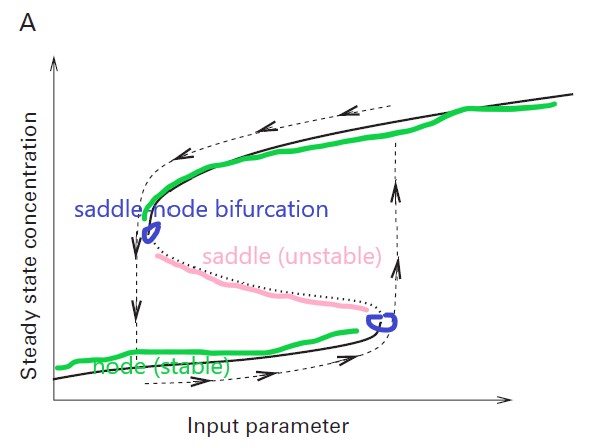
From Figure 4.20 A INGALLS B P. Mathematical modeling in systems biology: an introduction[M]. MIT press, 2013.
When considering changing one parameter in a non-linear network with positive feedback, we can observe saddle-node bifurcation and bistability under certain conditions.
The two bifurcation points define a bistable region with two stable fixed points. If we want to switch the system’s state by altering the input parameter, the state can only be switched until we go beyond the bifurcation point, as the black dashed line with arrows in the figure. This is what is called the hysteresis effect.
Bistable behavior
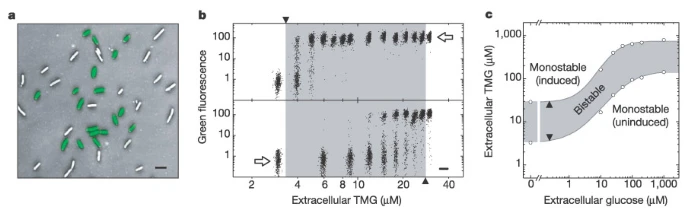
To observe the bistable behavior, we need to observe the single cells, or we can’t tell whether the transition is ‘switch-like’ or continuous when the bulk averages the effects. In a, researchers could indeed observe the two states, lac operon uninduced and fully induced.
In b, hysteresis was observed when altering the extracellular TMG concentration (keeping the extracellular glucose concentration zero). The switch was not ‘ideal’ because of stochastic effects.
In c, if we change another parameter, the extracellular glucose concentration, the bistable region will gradually change. Intuitively, lactose metabolism is harder to induce with abundant glucose since glucose seems a good choice of carbon source.
Model (Quantitative)
To quantitatively describe this network, researchers wrote down ODEs to describe the conceptual model. Check the supplementary information. After combining those ODEs, the solution of the Green Fluorescence could be written as
\[y=\alpha\frac{1+(\beta y)^2}{\rho+(\beta y)^2}\]where \(\alpha\) (the maximal activity) is the lac expression level that would be obtained if every repressor molecule were inactive; \(\rho\) (the repression factor) gives the ratio of maximal to basal activities; \(\beta\) (the transport rate) gives the TMG uptake rate per LacY molecule. These three parameters were unknown functions of the two input parameters of the network (the external concentration of glucose and TMG) and needed to be fitted from the experiments. Also, this is a non-linear equation which might have different numbers of real unequal solutions.
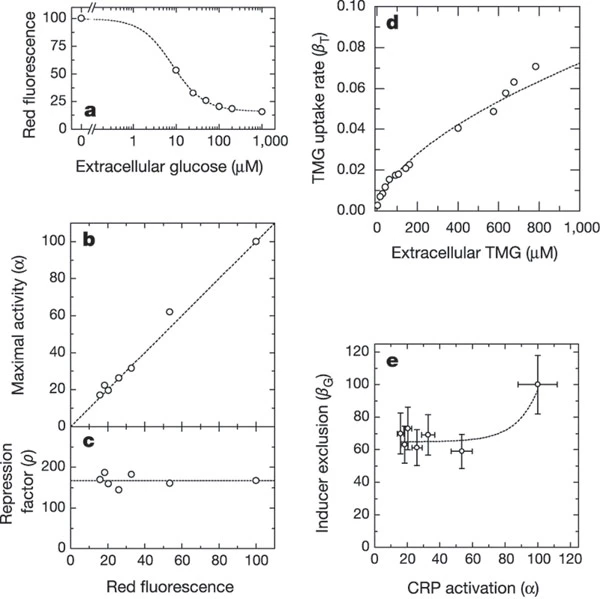
The figures above show how these parameters were fitted from the experiments. It is too tedious to explain them in detail. The main conclusions are \(\alpha\) is independent of TMG levels, suggesting the LacI and CRP bind independently to the lac operator site; \(\rho\) is a constant which is independent of levels of TMG or glucose; \(\beta\) can be written as a product of a pure function of TMG levels and a function of glucose level.
These parameters give us insight of the mechanism of biological processes, and also let us quantitatively analyze the solution given by the ODEs.
Synthesis type with a critical point where bistablity vanishes
From above, there is always a bistable region in wild-type E. coli, regardless of how the input parameters are altered, and \(\rho\) is a constant. However, if we decrease \(\rho\), we may find the bistable region shrinks. Eventually, the three fixed points (two stable nodes and the saddle, three unequal real solutions) collide and become one stable fixed point (one unequal real solution). Researchers could alter \(\rho\) by introducing more plasmids with LacI-binding sites to reduce the effective repression factor.
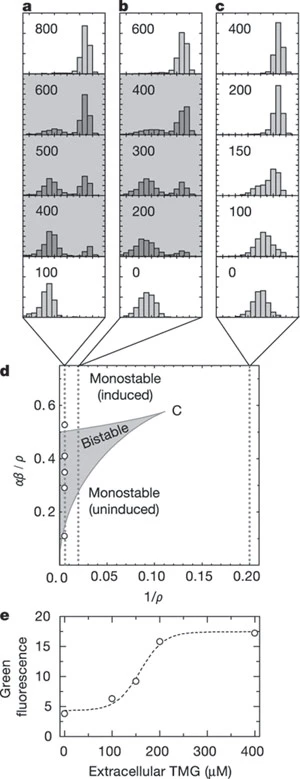
Therefore, researchers construct models with different values of $\rho$. In a and b, we can observe the existence of bistable regions, while in c, we can only observe monostability (the x-axis of histograms is the green fluorescence). e shows in c case, the green fluorescence is a gradually changing function of the extracellular TMG. The authors made an analogy to phase transitions in thermodynamics, which is interesting.
文档信息
- 本文作者:L Shi
- 本文链接:https://SHI200005.github.io/2023/04/21/Lactose-Network/
- 版权声明:自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)