热学有宏观描述方法(热力学方法)与微观描述方法(统计物理学方法)之分。这一篇首先将热力学,是关于热现象的宏观理论,把物质当作连续介质,以三条基本定律作为基础作演绎推论。
| 课程名称 | 热学 |
| 学习时间 | 大一下 |
| 周课时 | 3 |
| 本人成绩 | 97 |
| 课程教材 | 秦允豪等 《热学》高等教育出版社 |
| 个人建议参考教材 | 同上 |
| 先修课程 | 微积分 概率论 数理统计 |
上一篇力学和本篇热力学研究对象的不同在于,前者研究“时间之矢可以逆转”的过程(牛顿第二定律支配下的宏观物体作为研究对象),后者研究前者研究“时间之矢不可以逆转”的过程(必须建立描述宏观物体过程以外的新规律才能描述的过程)。
Hat alles seine Zeit: Das Nahe wird weit, Das Warm wird kalt, Der Junge wird alt, Das Kalte wird warm, Der Reiche wird arm, Der Naare gescheit, Alles zu seiner Zeit. – J. W. v. Goethe
平衡态与稳态
平衡态:在不受外界条件影响下,经过足够长时间后系统必将达到一个宏观上看来不随时间变化的状态,这种状态称为平衡态。无热流(热学平衡)、粒子流(力学平衡、化学平衡)。
稳态:我们把在有热流或粒子流情况下,各处宏观状态均不随时间变化的状态称为稳态。
热力学第零定律 - 引入温度
热平衡定律:在不受外界影响的情况下,只要 A 和 B 同时与 C 处于热平衡,即使 A 和 B 没有热接触,它们仍然处于热平衡状态。(key point: the existence of a function that constrains the parameters of each system in thermal equilibrium,参见 Kardar)
those constrains(显含温度 \(T\) 的物态方程)-> 温度和温标(理想气体温标其实就是热力学温标)
温度的统计意义:温度标志着物体内部分子热运动的剧烈程度,它是大量分子热运动平动动能的统计平均值的量度,\(\displaystyle\bar{\epsilon_k}=\frac{3}{2}kT\)。
温标的国际单位制是怎么确定的?标准:水的三相点——水的三相共存状态的温度是 273.16 开尔文。那么问题来了,水三相共存的温度怎么是唯一的?详见下文。
理想气体物态方程
理想气体:压强趋于零的极限状态下。物态方程:\(pV=nRT\)。不同种类都一样 -> 理想气体分压定律。适用范围:在常温下,压强在数个大气压以下的气体,一般都能很好地满足理想气体物态方程。模型的三个假定(除此之外还要有混沌性精神):
- 分子线度比分子间距小得多,可忽略不计。
- 除碰撞一瞬间外,分子间相互作用力忽略不计。分子两次碰撞之间做自由匀速直线运动。
- 处于平衡态的理想气体,分子之间以及分子与器壁之间的碰撞是完全弹性碰撞。
分子热运动。布朗运动。涨落。
分子相互作用势能曲线。范德瓦尔斯方程:理想气体中只有动理压强,而真实气体中除了有动理压强外还应有由于分子间作用力产生的压强,\(\displaystyle (p+n^2\frac{a}{V_m^2})(V-nb)=nRT\)。重要意义:能同时描述气体、液体及气液相互转变的性质,也能说明临界点的特征,从而揭示相变与临界现象的特点。
输运现象
分子动理学理论的非平衡态理论(近平衡态)。以下讨论的应该都属于线性理论,即引起偏离平衡态的各种热力学力比较小,由这些“力”所产生的各种热力学流与“力”之间遵从线性关系。介绍一些经验公式,其中菲克定律我现在接触比较多。参见 David Tong: Lectures on Kinetic Theory - 1.3.2。于是,这些线性理论给出线性微分方程,部分特别“简单”的在数学物理方程中被求解。
- 黏性现象:牛顿粘性定律 \(\displaystyle f=-\eta\frac{du}{dz}A\)、泊肃叶定律 \(\displaystyle \frac{dV}{dt}=\frac{\pi r^4\Delta p}{8\eta L}\)(动脉粥状硬化和高血压的联系)、斯托克斯定律 \(f=6\pi v \eta r\)(挺难推的,可以参考梁昆淼老师《理论力学》13.7.2,我还没看)。
- 扩散现象:概率流与浓度差的联系 \(\vec J=-D\nabla C\)(菲克定律),物质守恒 \(\displaystyle\frac{\partial C}{\partial t}=-\vec\nabla\cdot\vec J\);结合得到扩散方程 \(\displaystyle\frac{\partial C}{\partial t}=D\nabla^2 C\)。事实上,这正是随机游走的宏观体现。
- 热传导现象:傅里叶定律 \(\vec q=-k\nabla u\)——联系热容、温度变化和能量守恒。
- 对流传热:牛顿冷却定律 \(\dot Q=-hA(T-T_0)\)。
热力学第一定律 - 引入内能
准静态、可逆与不可逆过程。只有无耗散的准静态过程才是可逆过程。
- 热力学第一定律的数学表达式(重要!)
- \(U_2-U_1=Q+W\) 热力学第一定律一般表达式 能量守恒 量化「热量」
- \(dU=\bar{d}Q+\bar{d}W\) 无限小过程第一定律表达式,\(\bar dW=\displaystyle\sum_i J_idx_i\). 广义力-广义位移
- \(\bar dU=\bar dQ-pdV\) 对于理想气体体积功可逆过程。
等体过程、绝热过程、等温过程、等压过程在 \(V-p\) 图上的曲线。注意,这里所谈论的都是可逆过程,否则不平衡状态无法在 \(V-p\) 平面描绘。将这些过程带入热力学第一定律求解,是本章习题的一大考察内容。e.g., 绝热过程泊松公式 \(pV^\gamma=C\),其中 \(\displaystyle \gamma=\frac{C_{p,m}}{C_{V,m}}\)。
焓 \(H=U+pV\)。\(\displaystyle c_V=(\frac{\partial u}{\partial T})_V\)。\(\displaystyle c_p=(\frac{\partial h}{\partial T})_p\)。
- 热机
- 卡诺热机:2 等温 2 绝热过程的可逆循环 -> 卡诺热机的效率 \(\displaystyle\eta_{可卡}=1-\frac{T_2}{T_1}\) -> 后续的卡诺定理
- 内燃机循环:Otto循环、Dissel 循环。由飞轮循环贯穿起来的一系列冲程。
-
制冷机
焦耳-汤姆孙效应。绝热条件下,高压气体经过多孔塞、小孔、通径很小的阀门、毛细管等流到低压一边的稳定流动过程称为节流过程。绝热节流过程前后的焓不变。.
热力学第二定律 - 引入熵
-
开尔文表述:一切热机不可能从单一热源吸热把它全部转化为功而不产生其它影响。
克劳修斯表述:不可能把热量从低温物体传到高温物体而不产生其他影响。
两种表述等价。以及后续一些论断是通过“与热力学第二定律的某种表述相悖”而成立的。
卡诺定理(可逆热机,效率有最大值)\(\displaystyle\eta_任<\eta≤1-\frac{T_2}{T_1}\) -> 克劳修斯等式 \(\displaystyle\oint_{可卡}\frac{\bar dQ}{T}=0\) 这里热力学第二定律正是在卡诺定理的基础上推出的。
-
状态函数熵 \(\displaystyle S_b-S_a=\int_{a可逆}^b\frac{\bar dQ}{T}\) -> 克劳修斯不等式(热力学第二定律的数学表述)\(\displaystyle S_b-S_a\geq \int_a^b\frac{\bar dQ}{T}\).
对于无限小过程,\(TdS=(\bar dQ)_{可逆}\)
结合热力学第一定律和第二定律得到热力学基本微分方程,仅适用于可逆变化过程,只有体积功 \(dU=TdS-pdV\) (重要,统计物理我将从这里开始)
如果不幸需要求解不可逆过程的熵变怎么办?拿就构造假的可逆过程,讲初态和末态连接起来,求解这个假的可逆过程的熵变。熵是状态函数,跟具体的过程无关。
熵增加原理:在不可逆绝热过程中熵总是增加的;可逆绝热过程中熵不变。\(\displaystyle dS≥\frac{\bar d Q}{T}\)(注意:对于不可逆过程,\(T\) 是热源温度)。
参考阅读《从卡诺定理到熵增加原理》。
补充:来自 Kardar,参见下面粒子数可变系统。\(dE=TdS+\vec{J}· d\vec{x}+\vec{\mu}·d\vec{N}\)(热力学基本方程)。被微分的都是广延量。数学操作广延性后,\(E=TS+\vec{J}· \vec{x}+\vec{\mu}\vec{N}\)(热力学基本方程更基本,广延性来自系统中相互作用是短程的假设)。联立得约束条件 \(SdT+\vec{x}· d\vec{J}+\vec{N}·d\vec{\mu}=0\)。为啥提这个?回答吉布斯相律 e.g., 水的三相点为什么是个点(见大学化学)。
温度、内能、熵是基本热力学函数。熵能够用于判定绝热过程不可逆方向。对于非绝热过程,可以构造一个更大的绝热系统。然而,从克劳修斯不等式出发构造新的态函数用于判定不可逆方向更方便(平衡时该热力学函数取极值)。对于等温等容过程可以构造自由能 \(F=U-TS\)(参见林书1.13.1),对于绝热等压过程可以构造焓 \(H=E-pV\),对于等温等压过程可以构造吉布斯自由能 \(G=U-TS+pV=F+pV\)。焓、自由能、吉布斯自由能是辅助热力学函数。各自条件下,达到平衡时辅助热力学函数取极值(例:可逆等温过程系统对外界所作功为最大,它等于系统自由能的减少;如果为等容过程,则自由能无法增加)。体会一下“自由”二字的含义~
- 如果你从事生物物理,那么对你来说最重要的热力学函数便是吉布斯自由能,原因是我们一般处理等温等压的情况,而等温等压 \((T,p)\)下系统平衡条件与吉布斯自由能相关。为什么吉布斯函数能成为化学平衡的判据?为什么不是内能,如何理解这一现象?
| 课程名称 | 热力学与统计物理 |
| 学习时间 | 大三下 |
| 周课时 | 4 |
| 本人成绩 | 74 本来是61 |
| 课程教材 | 汪志诚 《统计物理学》 |
| 个人建议参考教材 | 1. Mehran Kardar, Statistical Physics of Particles 2. 《热力学与统计物理学》林宗涵 |
| 先修课程 | 微积分 概率论 数理统计 热学 近代物理 量子力学 |
均匀系的平衡性质
自然变量:如果适当选择独立变量(称为自然变量),只要知道一个热力学函数及它的自然变量,就可以通过求偏导而求得均匀系的全部热力学函数,从而把均匀系统的平衡性质完全确定。
学习热力学,就是经常把热力学量变来变去,有时目的是用可测量量表示热力学量以确定热力学量。可测量量一般可以概括为状态变量(如压强、温度…)和响应函数(如热容、“广义热容”)。
怎样巧记麦克斯韦关系? - 愛物理的无双麓叶的回答 - 知乎。考虑 \(p-V-T\) 系统,利用勒让德变换,由 \(dU, dH, dF, dG\) 四个微分式分别可以导出4个麦克斯韦关系。(物理的热力学基本方程+数学的微分关系对应,然后再求一次偏导…)
| 基本微分方程的等价形式 | 自然变量 | 麦克斯韦关系 |
| \(dU=TdS-pdV\) | \((S,V)\) | \((\frac{\partial T}{\partial V})_S=-(\frac{\partial p}{\partial S})_V\) |
| \(dH=TdS+Vdp\) | \((S,p)\) | \((\frac{\partial T}{\partial p})_S=(\frac{\partial V}{\partial S})_p\) |
| \(dF=-SdT-pdV\) | \((T,V)\) | \((\frac{\partial S}{\partial V})_T=(\frac{\partial p}{\partial T})_V\) |
| \(dG=-SdT+Vdp\) | \((T,p)\) | \((\frac{\partial S}{\partial p})_T=-(\frac{\partial V}{\partial T})_p\) |
麦克斯韦关系的简单应用(见热力学 - 均匀系统的热力学性质)
- 导出用可测量量表示的物理量偏导,目前感觉没啥用,不讲。
- 导出热辐射的热力学理论。特性:\(U(T,V)=u(T)V\), \(p=(1/3)u\) -热力学基本方程+麦克斯韦关系+黑体辐射压强 -> 结论:\(u=aT^4\), \(S=4/3AT^3v\), \(G=0\)。物理意义:热辐射的化学势为零,微观上代表热辐射的光子数不守恒,完全是唯象热力学理论导出的(见下面 相变的热力学理论-热动平衡判据-平衡条件)。
- 获得低温的方法:准静态实际气体的节流过程(需要 \(\displaystyle (\frac{\partial T}{\partial p})_H<0\),因为理想气体=0)、绝热膨胀过程(\(\displaystyle(\frac{\partial T}{\partial p})_S>0\))。顺磁性固体的磁冷却法(\(\displaystyle(\frac{\partial T}{\partial \mathscr{H}})_S>0\))。
相变的热力学理论
热动平衡判据
-
不同系统的稳定平衡判据(互为充要条件),热力学第二定律的推论。
粒子数不变的系统
熵判据:孤立系统(内能、体积不变的封闭系统) <-> \(S\) 取极大值
亥姆霍兹自由能判据:温度、体积不变的的封闭系统 <-> \(F\) 取极小值
吉布斯自由能判据:温度、压强不变的的封闭系统 <-> \(G\) 取极小值 重要!
内能判据:熵和体积不变的封闭系统 <-> \(U\) 取极小值
粒子数可变的系统
化学势的导出与热力学量的推广。引出物理量巨势 \(\Phi(T,V,\mu)=F-G\),相变平衡时取巨势取极小值。

-
平衡条件
热力学函数一阶微分等于 0 -> 热动平衡条件:子系 \(T\) 相等;力学平衡条件:子系 \(p\) 相等;相变平衡条件:子系 \(μ\) 相等。
热力学函数二阶微分正负 -> 平衡的稳定性条件:\(c_v>0\), \(\displaystyle (\frac{\partial p}{\partial v})_T>0\), \(c_p>0\), \(\displaystyle (\frac{\partial v}{\partial p})_T<0\).
粒子数可变系统化学势为 0:\(\delta F=-(p_1-p_2)\delta V_1+\mu_1\delta N_1+\mu_2\delta N_2\),因为没有粒子数守恒的约束,\(\delta V_1,\delta N_1,\delta N_2\) 相互独立 -> \(p_1=p_2,\mu_1=\mu_2=0\)。
-
单元系(化学纯物质)的复相平衡
\(\mu^\alpha(T,p)\) 两相平衡曲线、三相点。
克拉珀龙方程 \(\displaystyle \frac{dp}{dT}=\frac{\lambda_{\alpha\beta}}{T(v_\alpha-v_\beta)}\) 给出平衡曲线的斜率和相变潜热的关系,适用于有体积变化、有相变潜热的一级相变。
-
气-液相变与临界点
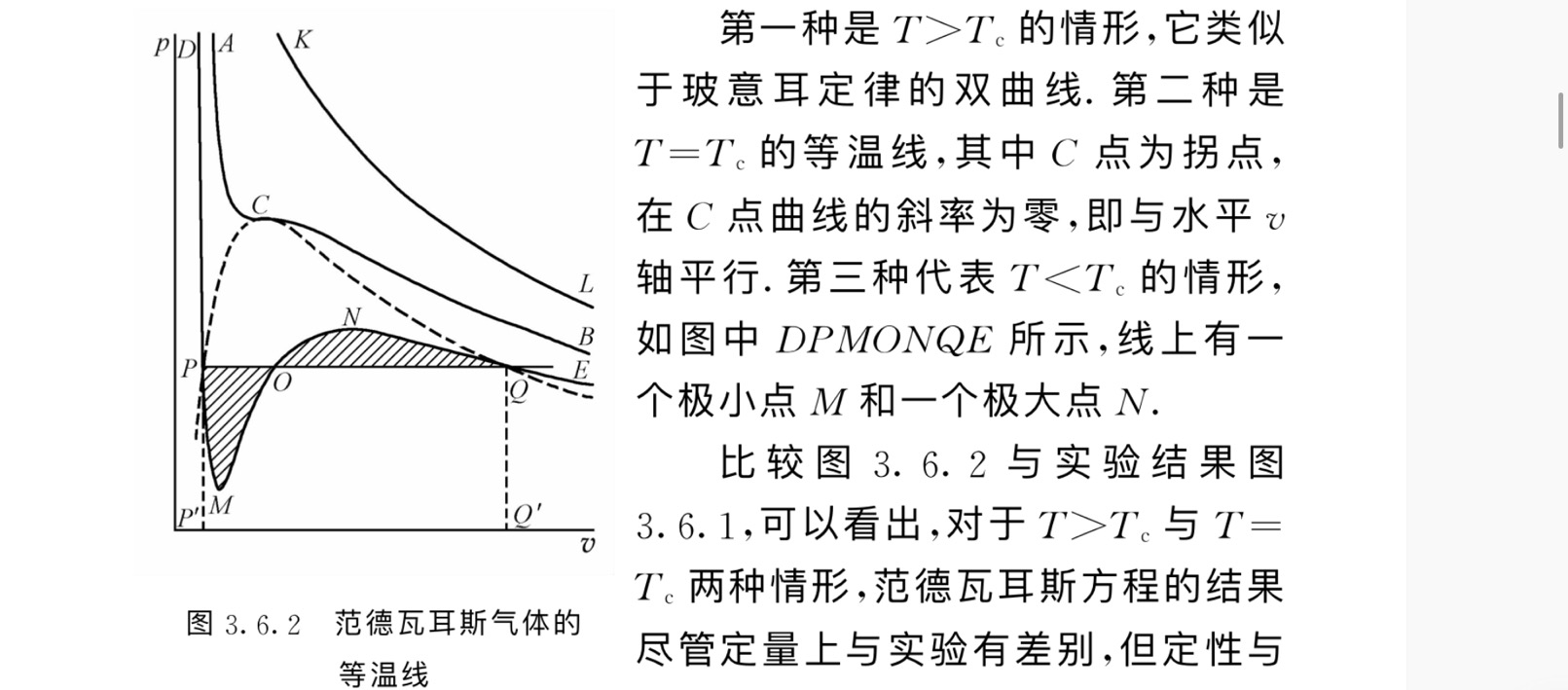
范德瓦尔斯气体方程(见热学)等温线 :有一段不符合平衡的稳定条件! -> 正确地确定与稳定平衡态对应的气-液两相共存线的压强值:麦克斯韦等面积法则
临界点是等温线的拐点,一阶导二阶导都为零(属于二级相变) -> 对应态定律
-
正常-超导相变
分析正常相(N)和超导相(S)的吉布斯自由能函数,在超导相带入迈斯纳效应(超导体的完全抗磁性),得到 \(\displaystyle G_S(T,\mathscr H)-G_N(T,\mathscr H)=\frac{\mu_0}{2}[\mathscr H^2-\mathscr H^2_c(T)]\)。结论:若 \(\mathscr H>\mathscr H_c\),N 相稳定,vice versa。有磁场作用下是一级相变,没有磁场作用下是二级相变。
-
相变的分类
一级相变:在相变点,两相的化学势相等,但化学势的一级偏微商不相等。变既有相变潜热又有体积变化。在相变点允许两相共存,而且可以有亚稳态。eg., 固-液相变;固-气相变;固态不同相(不同晶格结构)之间的相变;气-液相变(临界点除外),等等。
-
二级相变:在相变点,两相的化学势和化学势的一级偏微商全部相等,但化学势的二级偏微商不相等(有界或者无穷大)。既无相变潜热,又无体积变化。没有两相共存(在临界点,两相合二为一);也没有亚稳态。eg., 液氦的超流相与正常相之间的转变;超导-正常相变(无外磁场时);铁磁-顺磁相变(无外磁场时);合金的有序-无序相变;等等。
如果二阶偏微商有界,用洛必达法则处理克拉珀龙方程得到埃伦费斯特方程。
-
序参量、对称性破缺。自由能在临界点附近展开,并应用自由能极小的条件求出序参量的解。举例:顺磁-铁磁相变。外磁场不为零但很小的情形可以求得磁化率等。
序参量的涨落 -> 平均场理论的适用条件:金兹堡判据
-
临界指数
在临界点邻域,某些热力学量 \(f(\epsilon)=A\epsilon^\lambda\{1+B\epsilon^x+...\} (x>0)\),其中 \(\epsilon=\frac{T-T_c}{T_c}\),\(f(\epsilon)\) 是热力学参量。\(\lambda\) 就是热力学参量。
由于朗道二级相变理论和范德瓦尔斯理论都是平均场理论,两种相变具有相同的临界指数。在 (En) Advanced Statistical Mechanics 中的伊辛模型平均场解中,也给出了相同的临界指数。
热力学第三定律
见林宗涵4.7。跟前面几节没太大关系。
能斯特定理
从低温化学反应中总结出汤姆生-伯特洛规则:在等温等压条件下,低温化学反应向着放热的方向进行。热力学理论:在等温等压条件下,过程应该向着吉布斯函数减少的方向进行。吉布斯 argument:引入相切假设(低温时化学亲和势与反应热相切)后,可以导出能斯特定理 \(\displaystyle\lim_{T\rightarrow0}(\Delta S)_T=0\)。更强的定理:\(\displaystyle\lim_{T\rightarrow0}S_T=0\)。
能斯特定理的实验证实。测量的过程和结果见下图(Kardar Eq.1.79)。
能斯特定理的一个推论:热容 \(\displaystyle\lim_{T\rightarrow 0} C_{\vec X}=0\)。事实上,热力学第三定律是量子效应的宏观体现。在统计物理中的二能级系统中,就有这样的肖特基热容行为。
文档信息
- 本文作者:L Shi
- 本文链接:https://SHI200005.github.io/2022/02/24/Thermodynamics/
- 版权声明:自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)