用概率描述的目的来源于对事实的不确定性。理论上,可以根据我们对事实(并不完全的认识的)知识给出一件事发生的(可能并不准确的)概率,用于权衡利弊。这个概率的真实性需要通过这个事件实际发生的频率核实。当我们关于事实的知识改变时,可能这个理论上的概率值也将改变。在 (En) Machine Learning 和之后的 (En) Information Theory 中,将会有更深的体会。
本想复习完微积分与线性代数后先开始复习力学与热学,不过预见到不久后的实践中会用到概率论,以及其实暑校的(尝试)主元分析实践中已经用到概率论,所以或许该早点复习。关于相关知识的重要性,我可以贴一个有趣的TED视频,非常简短,无干货,有趣而已。TED演讲:先教统计学再教微积分!
2024.04.29 更新:相关科普书:The Drunkard’s Walk: How Randomness Rules Our Lives.
事实上,这门课可能是最为重要的一门课(尤其是日后转到其他定量科学领域)。同时,作为9-11节的晚间专业选修课,这门课也是一门绝对的水课。如果我早点意识到这门课对我的重要性和修读课程的水性,早点开始自学,就不会走这么多弯路了。
更新记录 2021.10.02 Ver0.0, 2021.11.09 Ver0.1, 2021.11.17 Ver0.2, 2022.11.12 Ver1.0, 2022.11.23 Ver1.1, 2023.10.14 Ver1.2 (law of weak large number, generating functions)
| 学习时间 | 大二上 |
| 周学时 | 3 |
| 本人成绩 | 94 |
| 课程教材 | 名存实亡 已绝版… |
| 个人建议参考教材 | 本人这篇 |
| 先修课程 | 微积分 线性代数 复变函数 |
External References
- Kardar, Mehran. Statistical physics of particles. Cambridge University Press, 2007.
- Van Kampen, Nicolaas Godfried. Stochastic processes in physics and chemistry. Vol. 1. Elsevier, 1992.
概率论的基本概念
等可能概型(古典概型)
条件概率
\(\displaystyle P(A|B)=\frac{P(A,B)}{P(B)}\) 很重要!
全概率公式与Bayes 公式
- \[\displaystyle P(B_i|A)=\frac{P(A|B_i)P(B_i)}{\sum_{j=1}^{n}P(A|B_j)P(B_j)}\]
-
可用于求解后验概率(在得到信息之后再重新加以修正的概率),利用条件概率公式联系后验概率和先验概率
先验概率:已知的信息;后验概率:给已知信息后对认知进行修正。【Intuition】测试结果为阳性的人是感染者的概率 <-> 感染者的检测结果是阳性的概率。
【GRAD-UPDATE】在 (En) Machine Learning 相关理论的重要背景。
独立事件
若 \(A, B\) 互为独立事件,则 \(P(A,B)=P(A)P(B)\), \(P(A\vert B)=P(A)\).
随机变量及其分布
离散型随机变量
二项分布
\[X\sim b(n,p)\]\(n\) 重伯努利试验 -> 二项分布
泊松分布
\[X\sim π(λ)\]泊松分布作为泊松过程的“某时段内发生事件数”的分布。泊松过程中事件发生的等待时间间隔服从指数分布(详见“连续型随机变量–指数分布”)。泊松分布与指数分布的联系。【SELF-STUDY】泊松分布可以从非常少的假设(独立发生、无聚束效应)推导出来。本人知乎文章(搬运《数学动力学模型》)泊松分布与泊松过程。
泊松分布作为二项分布的近似:\(n\) 很大而 \(p\) 很小 -> \(X\sim b(n,p)\)-> \(X\sim π(λ)\), \(λ=np\).(\(n\) 很大的话,算阶乘程序肯定会死)。证明很简单,详见概率论-泊松分布作为二项分布的近似。Intuition: 用泊松过程推导泊松分布的时候,就是从一件事发生还是不发生出发,取时间间隔的极限小,也就是考虑极限情况下做伯努利试验成不成功,所以是二项分布的极限情况。
【GRAD-UPDATE】从一个泊松过程中随机选取一些事件(选取的概率是常数 \(r\)),这些事件依然构成泊松过程。
【GRAD-UPDATE】泊松过程的适用条件:试想一个任意的过程,从该过程中随机地选取极少的事件。事件之间的相关性随时间衰减,如果选的事件足够稀少,那么选出的事件可以近似地用泊松过程描述。
【GRAD-UPDATE】本科阶段只讨论了事件发生概率是常数 \(r\) 的情况,结论是一段时间 \(T\) 内发生事件的计数 \(N\) 满足 \(\langle N\rangle=rt\),\(\langle N^2\rangle=\langle N\rangle\). 考虑更一般的情况,事件发生概率 \(r(t)\) 随时间变化,但是各个事件的发生没有关联,有结论 \(\displaystyle\langle N\rangle=\int_0^Tdt r(t)\),\(\langle N^2\rangle=\langle N\rangle\)。文章详见泊松分布与泊松分布(II),推导过程详见概率论-一般的泊松过程与泊松分布。
【GRAD-UPDATE】一维随机游走(birth-and-death)过程中,细致平衡给出稳态时系统在稳态“格点”附近的分布也是泊松分布。为什么呢?因为 bounded 泊松过程给出泊松分布(详见我的博士学位论文?)
几何分布
【GRAD-UPDATE】在伯努利实验中,得到一次成功所需要的试验次数分布。
在生物物理实验数据中描述多态动力学的 burst-size distribution。
连续型随机变量
分布函数 c.d.f.(数学家更喜欢,考虑到有离散情况的数学形式)、概率密度 p.d.f.(物理学家更喜欢,与统计系综的概念联系紧密,相信信息学家也更喜欢这个)。
均匀分布
\[X\sim U(a,b)\]指数分布
指数分布具有无记忆性。闲聊:知乎网友指数分布的分布函数是怎么得到的?。
泊松分布与指数分布的联系:符合泊松分布的两个事件发生时间间隔符合指数分布。
正态分布(高斯分布)
(\(X\)~\(N(μ,σ^2)\))
正态分布作为二项分布的近似:\(n\) 很大,\(p\) 接近 \(1/2\) -> \(X\sim b(n,p)\) -> \(X\sim N(μ,σ^2)\)。【GRAD-UPDATE】结论来自于求解 Fokker-Planck 近似下的小偏差(\(p\) 接近于 \(1/2\))的概率偏微分方程,需要用到傅里叶变换,详见随机过程。
知乎网友关于泊松分布与正态分布作为二项分布的近似的定量刻画工作定量理解二项式分布的泊松和高斯近似。
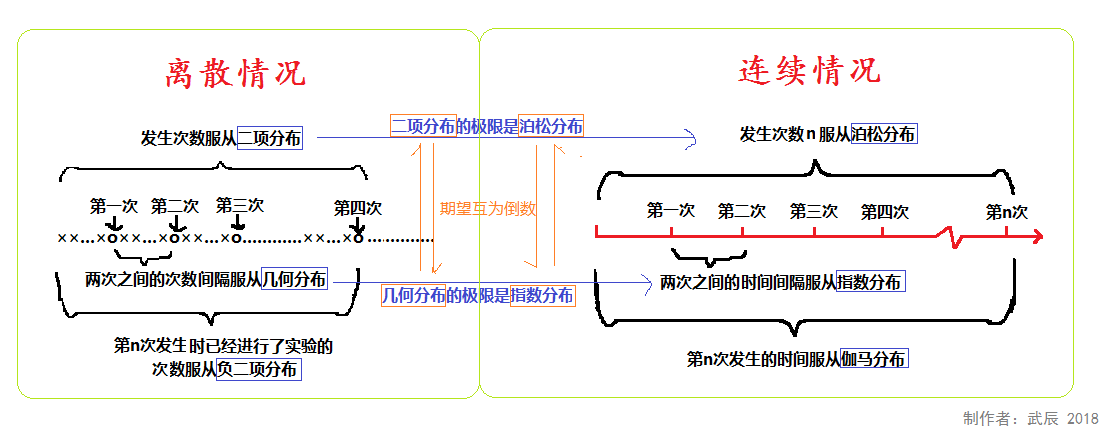
关于更多随机变量分布概率分布。一张图说明二项分布、泊松分布、指数分布、几何分布、负二项分布、伽玛分布的联系。
随机变量和的分布
如果随机变量 \(X_1\sim P_1\) 和 \(X_2\sim P_2\) 相互 独立,则 \(X=X_1+X_2\) 的分布函数为
连续:\(P(X=x)=\displaystyle\int_{all} P_1(X_1=u)P_2(X_2=X-u)du\)
离散:\(P(X=x)=\displaystyle\sum_{all} P_1(X_1=u)P_2(X_2=X-u)\)
注意,我们在这里看到了卷积,于是想到了傅里叶变换的卷积定理(详见复变函数)。
结论
泊松 + 泊松还是泊松,参数为求和。
-
多个相同指数分布随机变量的和
【GRAD-UPDATE】Erlang Distribution: 产生于电话接线背景,可以用于描述生物信号转导中的 N-Step Cascade,每一步都是指数分布。指数分布在均值处没有峰值,是个乱七八糟的分布,但是如果多步级联(几个随机变量的和),就不那么乱七八糟了。
Example in biophysics: analytical continuous model solution of protein distribution when produced in bursts, and the burst size obeys the exponential distribution. Reference: Friedman, N., Cai, L., & Xie, X. S. (2006). Linking stochastic dynamics to population distribution: an analytical framework of gene expression. Physical review letters, 97(16), 168302. online Note that Laplace transform (see 复变函数) was applied to solve it.
The exponential distribution, Erlang distribution, and chi-squared distribution (encountered in 数理统计) are special cases of the gamma distribution.
已知一个随机变量为指数分布,与另一个随机变量的和为指数分布,另一个随机变量是指数分布吗?不是。见 Thomas & Cover Elements of Information Theory 习题 9.3。
正态 + 正态还是正态,期望为期望和,方差为方差和,证明:Sum of normally distributed random variables。
如果两个正态分布的随机变量有相关性,则它们的和还是高斯分布,期望为相加,方差并非简单相加。推导见上面的链接。
常见分布的关系
泊松分布(参数 \(\lambda\))被伯努利挑选(概率 \(p\))后,仍为泊松分布(参数 \(p\lambda\))。证明从略。
多维随机变量及其分布
联合分布
以二维随机变量为例 \(F(x,y)=P\{(X≤x)∩(Y≤y)\}=P\{X≤x, Y≤y\}\)
- 连续型随机变量联合概率密度 \(\displaystyle F(x,y)=\int_{-∞}^y{f(u,v)dudv}\), \(\displaystyle\frac{\partial^2{F(x,y)}}{\partial x\partial y}=f(x,y)\).
Multivariate Gaussian Distribution
\[G(\mathbf {x})=\displaystyle (2\pi )^{-k/2}\det({\boldsymbol {\Sigma }})^{-1/2}\,\exp \left(-{\frac {1}{2}}(\mathbf {x} -{\boldsymbol {\mu }})^{\!{\mathsf {T}}}{\boldsymbol {\Sigma }}^{-1}(\mathbf {x} -{\boldsymbol {\mu }})\right)\]其中 \(\mathbf {x}\) 是 \(k\) 维随机变量摞成的一个列向量。问题:为什么指数部分取协方差矩阵的逆?其实不用太繁琐的数学推导——Hint: 协方差矩阵是实对称矩阵,能够合同对角化(线性代数),然后请自行对随机变量进行基变换,你会明白。
边缘分布
以二维随机变量为例 \((X,Y)\) 关于 \(X\) 的边缘分布函数:\(P\{X≤x\}=P\{X≤x,y<∞\}=F(x,∞)=F_X(x)\)
已知联合分布可导出随机变量各自的条件分布,已知各自的条件分布不能导出它们的联合分布。
连续型随机变量边缘概率密度:\(\displaystyle f_X(x)=\int_{-∞}^{∞}{f(x,y)dy}\).
条件分布
\(p(y\vert x)=\displaystyle\frac{p(x,y)}{p(x)}\).
相互独立与两两独立
三个随机变量相互独立能推出三对随机变量两两独立,反之推不出。示例见下图,\(Z=X\oplus Y\),即布尔代数里的 XOR 运算。这一点在通信加密和解码中有应用(详见 (En) Information Theory)。

复合形式
\(p((z\vert y)\vert x)\) 其实就是 \(p(z\vert(x,y))\). (En) Information Theory 会用。
随机变量的数字特征
期望
\(E(X+Y)=E(X)+E(Y)\) 总成立
\(E(XY)=E(X)E(Y)\) 在 \(X,Y\) 相互独立时成立。
方差
定义:\(D(X)=Var(X)=E\{[(X)-E(X)]^2\}\).
- P.S. 并不是所有概率分布都存在有限的方差!例如 \(\displaystyle P(x)=\frac{1}{\pi}\frac{\gamma}{(x-a^2)+\gamma^2}(-\infty<x<\infty)\),也称为 Lorentz-Cauchy distribution 就没有。
常见离散型随机变量期望与方差的求解
【GRAD-UPDATE】离散随机变量分布中的二项分布、泊松分布和几何分布的均值和方差如何计算?在 UofT PHY2108 课上,Prof Anton Zilman 介绍了用 Generating function 计算二项分布的均值和方差。这个方法也适用于计算泊松分布和几何分布的均值和方差。具体过程见 Generating Functions。
Law of total expectation & law of total variance
(using conditional probability of different cases)
\(E(X)=E(E(X\vert Y))\) i.e. lives of light bulbs from different factories
\(Var(X)=E[Var(X\vert Y)]+Var(E[X\vert Y])\)
Related work in systems biology
- Huh, D., & Paulsson, J. (2011). Random partitioning of molecules at cell division. Proceedings of the National Academy of Sciences, 108(36), 15004-15009. online
- Hilfinger, A., & Paulsson, J. (2011). Separating intrinsic from extrinsic fluctuations in dynamic biological systems. Proceedings of the National Academy of Sciences, 108(29), 12167-12172. online
附录
| 种类 | 分布 | 数学期望 | 方差 |
| 离散 | 二项分布 \(P(X=m)=\binom{N}{m}p^m(1-p)^{N-m}\), \(X\in \mathbb{N_0}\) | \(np\) | \(np(1-p)\) |
| 离散 | 泊松分布 \(P(X=m)=\frac{x^m e^{-\lambda}}{m!}\) , \(X\in \mathbb{N_0}\) | \(λ\) | \(λ\) |
| 离散 | 几何分布 \(P(X=m)=(1-p)^{k-1}p\), \(X\in \mathbb{N_0}\) | \(\frac{1}{p}\) | \(\frac{1-p}{p^2}\) |
| 连续 | 均匀分布 \(f(X=x)=\frac{1}{b-a}\), \(X\in[a,b]\) | \(\frac{a+b}{2}\) | \(\frac{(b-a)^2}{12}\) |
| 连续 | 指数分布 \(f(X=x)=\lambda e^{-\lambda x}\) ,\(X\in[0,\infty)\) | \(\frac{1}{θ}\) | \(\frac{1}{θ^2}\) |
| 连续 | 正态分布 \(f(X=x)=\frac{1}{\sqrt{2\pi}\sigma}e^{\frac{-(x-\mu)^2}{2\sigma^2}}\), \(X\in(-\infty,\infty)\) | \(μ\) | \(σ^2\) |
- 泊松分布,真是个可爱的分布。法语小知识:Poisson 在法语里是🐟的意思。
随机变量的 fancy 数字特征
哈哈,这篇我本来想避免超出我们本科课程的范围,当时死记硬背不知所云的几个知识在引入一些数学上并不困难的新东西之后就变得很 intuitive 了。何乐而不介绍?
矩
矩还蛮重要的,英文叫 moment。
The characteristic function
(补充,参见 Kardar 2.2)
对概率分布做傅里叶变换(参见复变函数)得到 the characteristic function \(\displaystyle\tilde p(k)=\langle e^{-ikx}\rangle=\int dxp(x)e^{-ikx}\),then moments of the PDF around any point \(x_0\) can be generated by expanding \(e^{ikx_0}\tilde p(k)=\displaystyle\sum_{n=0}^\infty\frac{(-ik)^n}{n!}\langle(x-x_0)^n\rangle\)。
The cumulant generating function
(补充,参见 Kardar 2.2)
is \(\ln\tilde p(k)\),我们称把这个东西对 \(k\) 的展开项是 cumulants,Kardar 在书中用 \(\langle x^n\rangle_c\) 表示,van Kampen 在书中用 \(\langle\langle x^n\rangle\rangle\) 表示,维基百科中表示为 \(\kappa_n(x)\)。Why do we care about cumulants? 对于图形法背后的数学,在书中图形法的后一页解释得很清楚了,不再赘述。
An important theorem allows easy computation of moments in terms of the cumulants: represent the \(n\)th cumulant graphically as a connected cluster of \(n\) points. The \(m\)th moment is then obtained by summing all possible subdivisions of \(m\) points into groupings of smaller (connected or disconnected clusters).
高斯分布 \(\displaystyle p(x)=\frac{1}{\sqrt{2\pi\sigma^2}}exp[-\frac{(x-\lambda)^2}{2\sigma^2}]\) 的优良品质是 \(\langle x\rangle_c=\lambda\), \(\langle x^2\rangle_c=\sigma^2\), \(\langle x^3\rangle_c=\langle x^4\rangle_c=...=0\),也就是任何阶中心矩都可以用均值和方差两个参数表示。
得名:如果随机变量 \(x_i\) 相互独立,则 \(\displaystyle\kappa_n(\sum x_i)=\sum\kappa_n(x_i)\)。
上面这些单变量统计分布可以解决(更高级的去看(En) Advanced Statistical Mechanics),下面是多变量分布的简单性质。
协方差
定义:\(Cov(X,Y)=E\{[(X)-E(X)][(Y)-E(Y)]\}=E(XY)-E(X)E(Y)\).
\(D(X+Y)=D(X)+D(Y)+2E\{[(X)-E(X)][(Y)-E(Y)]\}\).
相关系数:\(\displaystyle ρ_{XY}=\frac{Cov(X,Y)}{\sqrt{D(X)}\sqrt{D(Y)}}\).(Term: Pearson correlation coefficient.)
协方差时二阶混合中心矩。协方差矩阵的定义…性质:证明:协方差矩阵是半正定矩阵,参见线性代数。
相关与独立
相关系数描述的是线性相关程度。性质是\(\vertρ_{XY}\vert≤1\),当且仅当 \(Y=a+bX\) 时取等号。若\(X,Y\) 独立,则相关系数一定为零;若相关系数为零,不一定独立。感觉这个名字有点误导性。
补充:概念:statistical independence 和 uncorrelated。
uncorrelated: \(ρ_{XY}=0\) (weaker than statistical independence)
statistical independence: expressed by any one of the three criteria:
- All moments factorize: \(\langle X_1^{m_1}X_2^{m_2}\rangle=\langle X_1^{m_1}\rangle\langle X_2^{m_2}\rangle\).
- The characteristic function factorizes: \(G(k_1,k_2)=G_1(k_1)G_2(k_2)\).
- The cumulants \(\langle\langle X_1^{m_1}X_2^{m_2}\rangle \rangle\) vanish when both \(m_1\) and \(m_2\) differ from zero. (the symbol for cumulants in van Kampen is different from that in Kardar, haha)
The reason why this property has a special name is that in many applications the first and second moments alone provide an adequate description (i.e. Gaussian distribution).
大数定理
大数定理
Chebyshev 不等式
Markov’s inequality: \(X\) non-negative, for every \(a>0\), \(\displaystyle P[X\geq a]\geq\frac{E[X]}{a}\).
Chebyshev’s inequality: arbitrary \(X\), \(Y=(X-E[X])^2\) thus non-negative, plug in Markov inequality, \(P\{\vert X-μ\vert\geq ε\}\leq\frac{σ^2}{ε^2}\), \(P\{\vert X-μ\vert<ε\}≥1-\frac{σ^2}{ε^2}\). 给出了在随机变量的分布未知,而只知道\(E(X)\)和\(D(X)\)的情况下估计概率的界限。
Note that 核心关系 \(\displaystyle D[\frac{1}{n}\sum_{k=1}^{n}{x_k}]=\frac{σ^2}{n}\), which means \(\sigma\)~\(N^{-1/2}\). Plug in Chebyshev’s inequality, we have For all \(\epsilon>0\) and all \(\delta>0\) there exists a positive integer \(n_0\) such that for all \(n\geq n_0\), \(P[\vert M_n-m\vert\geq\epsilon]\leq\delta\).
样本数增加,样本均值依概率收敛于随机变量均值。\(P[\vert M_n-m\vert\geq\epsilon]\rightarrow 0\) as \(n\rightarrow 0\).
伯努利大数定理
频率依概率收敛于概率(频率稳定性)。当试验次数很大时,便可以用事件的频率来代替事件的概率。
辛钦定理
与 Chebyshev:不需要方差存在。
与伯努利:伯努利是辛钦的特殊情况。
我根本看不懂这是在说什么。
中心极限定理
独立同分布的中心极限定理
独立同分布的中心极限定理:\(X\)~\(N(μ,σ^2)\) -> \(\bar{X}\)~\(N(μ,\frac{σ^2}{n})\) (Chebyshev 那里不是已经用到了,为啥再提![]() )
)
Lyapunov 定理
无论各个随机变量服从什么分布,只要满足定理的条件(the cumulants of the individual random variables are finite),那么它们的和当 \(n\) 很大时,就近似地服从正态分布。为什么呢?其实 Kardar 那本书的第二章讲得很清楚了。
Sum \(X=\displaystyle\sum_{i=1}^{N}x_i\), \(x_i\) are i.i.d. from a distribution. We have \(\langle X^n\rangle_c=N\langle x^n\rangle_c\). Construct \(\displaystyle y=\frac{X-N\langle x\rangle_c}{\sqrt N}\), so \(\langle y^n\rangle_c\propto N^{1-n/2}\). As \(N\rightarrow\infty\), only the second cumulant survives, and the PDF for \(y\) converges to the normal distribution, \(\displaystyle\lim_{N→\infty}p(y=\frac{\displaystyle\sum_{i=1}^N x_i-N\langle x \rangle_c}{\sqrt N})=\frac{1}{\sqrt{2\pi\langle x^2\rangle_c}}exp(-\frac{y^2}{2\langle x^2\rangle_c})\).
De Moiver-Laplace 定理
是中心极限定理的一种特殊情况。样本容量很大时,独立实验的成功概率接近 \(1/2\) 时,成功概率为二项分布,也就是所有成功事件的加和,可以通过斯特林公式(见统计物理)得到正态分布形式,详见随机过程。
文档信息
- 本文作者:L Shi
- 本文链接:https://SHI200005.github.io/2022/02/17/Probability/
- 版权声明:自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)